Matter Volume and Density Practice Problems and Review Worksheet Answers
Density Mass Volume
Density is a measure of how tightly the mass of an object is packed into the space it takes up. It can exist calculated past dividing mass by volume .
Brand sure yous are happy with the following topics before continuing.
- Rearranging Formulae
- Units and Conversions
Level 4-5 GCSE KS3 
Density Mass Book – Formula
Density , mass and book are all related by the formula,
d = \dfrac{thousand}{5}
where d is density , Five is volume , and one thousand is mass . This can be rearranged in gild to notice book or mass depending on which quantities you are given and what the question asks y'all to find.
Mass is ordinarily measured in grams, one thousand, or kilograms, kg, whereas, volume is normally measured in cubic centimetres, cm^3, or cubic metres, m^3.
This means when dividing mass by book, the resulting units are typically grams per cubic centimetre (g/cm^3), or kilograms per cubic metre (kg/m^3). These are chemical compound units (for more information, see conversions revision).
Level four-5 GCSE KS3
Density Mass Volume – Formula Triangle
A handy manner of remembering how to summate either density , mass or volume is to use the triangles below.
The horizontal line means carve up and the \times symbol ways multiply.
We then cover upward the one we want to detect (represented by a reddish circumvolve) and carry out the adding with the other 2 values from the triangle.
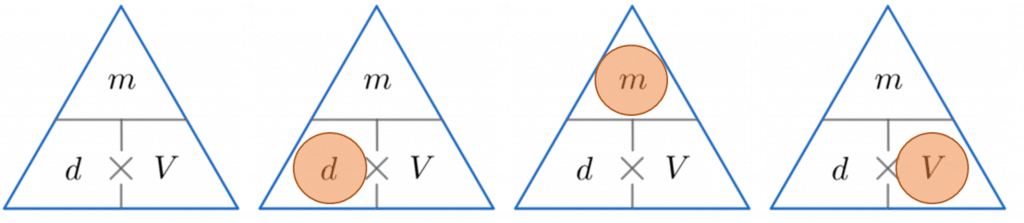Level four-5 GCSE KS3
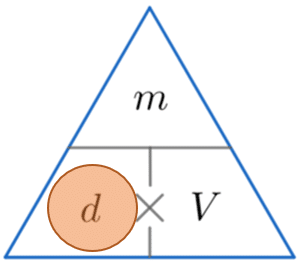
Example ane: Calculating Density
An object has a mass of 570 1000 and a book of 2280 cm^3. Calculate its density .
[2 marks]
We're looking for density, so constructing the triangle and covering d, we see we must divide the mass past the volume. So
\text{density } = \dfrac{570}{2280} = 0.25 k/cm^iii
Level four-5 GCSE KS3
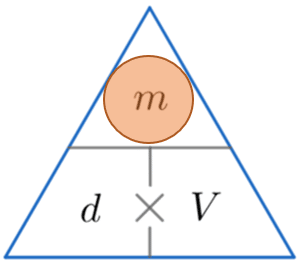
Example 2: Calculating Mass
A cat has volume 0.004 m^three and density 980 kg/m^iii. Calculate the mass of the true cat.
[2 marks]
We're looking for mass, so constructing the triangle and covering k, nosotros meet that to calculate the mass we must multiply the density by the book. Then
\text{ Mass } = 980 \times 0.004 = iii.92 kg
Level four-5 GCSE KS3
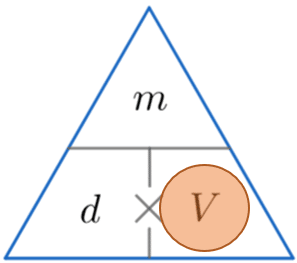
Example 3: Calculating Volume
A bottle of h2o has a density of grand kg/thou^3 and mass of 0.5 kg. Calculate the volume of the water bottle giving your respond in litres.
[2 marks]
Nosotros're looking for volume, then covering V, nosotros must carve up the mass past the density. So
\text{ Volume } = \dfrac{0.5}{grand} = 0.0005 m^3
Multiplying this by 1000 to convert into litres, gives the states the concluding answer,
\text{ Volume } = 0.5 50
Level 4-5 GCSE KS3
Example Questions
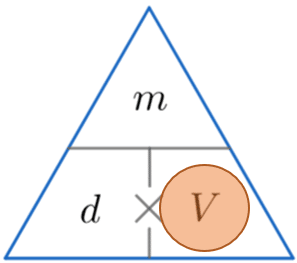
We are calculating the volume, so by covering upward the Five we can see from the triangle above that nosotros have to dissever m past d.
Before nosotros can do this, however, we take to make sure that we accept the correct units. The mass is in kilograms, but the density is in grams per cubic centimetre. This means that we accept to starting time convert the kilograms into grams before proceeding.
two kg = 2000 g
Therefore, the volume of the olive oil can exist calculated as follows:
\text{Book} = 2000 \div 0.925 = 2162cm^3
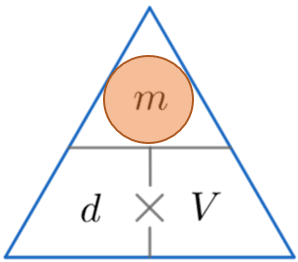
Nosotros are calculating the mass, and then by roofing up the m nosotros can see from the triangle above that nosotros have to multiply d by V.
However, we don't know the volume, but we practice know that the shape is a cube with a side length of 7 m, so the volume of the cube is:
seven \times vii \times 7 = 343 m^three
Now that we know the volume, we can multiply it by the density in order to calculate the mass:
\text{Mass } = 343 \times 10,800,000 = three,704,400,000 kg
To calculate the answer here, nosotros need to recall the formula:
\text{ density} = \text{ mass} \div \text{ book}
In this question, the mass is 2460kg and the volume is 1.two m^3, so we simply need to substitute these values into the formula every bit follows:
\text{ Density} = 2460 kg \div \, 1.ii chiliad^3 = 2050 kg/m^3
a) In order to summate the overall volume of the block, we need to add the book of metal A and the book of metal B. Although we don't accept the volume of either metal, we take been given their masses and densities, so nosotros can calculate the volume of each metallic appropriately.
Past rearranging the density formula, or using the triangle, we can work out how to calculate the volume:
\text{density} = \text{ mass}\div \text{ volume}
And then:
\text{volume} = \text{ mass}\div \text{ density}
The volume of metallic A can be calculated as follows:
1200 g \div \, five g/cm^iii = 240 cm^3
The book of metal B can be calculated as follows:
600 thousand \div \, 3 thou/cm^three = 200 cm^3
Therefore, if metal A has a volume of 240 cm^3 and B has a volume of 200 cm^iii, then their combined book is only:
240 cm^3 + 200 cm^three = 440 cm^3
b) Equally we know from question a), the newly-formed block has a volume of 440 cm^3.
We know that the mass of metal A was 1200 1000 and the mass of metal B was 600 g, then mass of the block is:
1200 one thousand + \, 600 g = 1800 g
The density of this block tin can be calculated by dividing the mass by the volume as follows:
1800 thousand \div \, 440 cm^three = four.09 thou/cm^3
This is quite a challenging question with a lot of calculations going on.
Since we have been given the mass of metallic C and the ratio of metal A and metal B in metal C, nosotros can therefore calculate the mass of metal A and metal B. If the ratio of metal A to metal B is 3 : 7, that means that \frac{3}{10} of the mass of metal C comes from metal A and the remaining \frac{vii}{10} is metal B. (We are dealing in tenths here since the sum of the ratio is 10.)
The mass of metallic A can exist calculated as follows:
2500 yard \times \dfrac{3}{x} = 750 yard
The mass of metal B can be calculated as follows:
2500 g \times \dfrac{seven}{ten} = 1750 g
We at present know both the mass and density of both metals A and B, meaning nosotros tin piece of work out their respective volumes.
Since
\text{density} = \text{ mass} \div \text {volume}
then
\text{volume} = \text{ mass} \div \text {density}
The volume of metal A can exist calculated equally follows:
750 g \div \, 3.2 g/cm^three = 234.375 cm^3
The volume of metallic A tin can be calculated as follows:
1750 grand \div \, 5.five m/cm^three = 318.18 cm^3
If metal A has a volume of 234.375 cm^3 and metal B has a book of 318.18 cm^iii, so their combined volume is the volume of metal C.
Volume of metallic C = 234.375 + 318.18 = 552.5568 cm^three
Nosotros at present know both the mass and volume of metal C, so we are now able to summate its density.
Density of metal C = 2500 g \div \, 552.5568 cm^3 = iv.five g/cm^iii
Related Topics
Worksheet and Example Questions
Drill Questions
Source: https://mathsmadeeasy.co.uk/gcse-maths-revision/density-mass-volume-gcse-revision-and-worksheets/
0 Response to "Matter Volume and Density Practice Problems and Review Worksheet Answers"
Post a Comment